

我們擅長商業策略與用戶體驗的完美結合。
歡迎瀏覽我們的案例。

我們所處的空間與時間,或許不是連續的?一個名為“圈量子引力”的量子理論,就提出了離散時空的概念。現在,一項由多位華人科學家主導的研究,讓該理論進入全新的階段——在實驗室中模擬圈量子引力中的時空量子態。
20世紀上半葉,量子理論的出現讓物理學進入全新的階段。這時,離散化成為物理學的新潮流。比如,玻爾通過對應原理計算出氫原子的電子能量是離散的,從而得出氫的光譜線;銀原子與不均勻磁場相互作用后,自旋角動量的方向也是離散的,這給出了斯特恩-蓋拉赫實驗中兩股銀原子飛行軌跡。
根據這個思路,一個很容易想到的問題是:既然能量與角動量都是量子化,也就是離散化的,那么時間與空間是不是離散的呢?
圈量子引力的誕生
一個誕生于1987年的全新理論,就提出了時空是離散的觀點。這種物理學思想,就是圈量子引力(loop quantum gravity)理論。
在圈量子引力出現之前,最流行的量子引力理論是惠勒-德威特方程。這個方程類似于量子力學的薛定諤方程:在惠勒-德威特方程中,整個宇宙空間可以看成波函數,這個波函數的演化滿足薛定諤方程。但是,惠勒-德威特方程存在很多問題,因此后來被淘汰了。
20世紀80年代中期,卡洛·羅韋利(Carlo Rovelli)和阿比耶·阿什特卡爾(Abhay Ashtekar)、李·斯莫林(Lee Smolin)開始重新考慮這個問題。他們在惠勒-德威特方程的基礎上,創建了圈量子引力理論。
羅韋利在接受《環球科學》采訪時,介紹了圈量子引力的誕生經歷:“1987年夏天,我還是一個對量子引力問題感興趣的年輕博士后,到處拜訪這個領域的科學家。當我去耶魯大學拜訪斯莫林時,他告訴我,他發現了惠勒-德威特方程的一些奇怪的解——在那里,空間中每個圈都有一個可能的解。于是,我開始和斯莫林合作。我們意識到,他的解可以成為量子引力的新基礎。”隨后,羅韋利和斯莫林去了美國錫拉丘茲大學,和當時在該校任職的阿什特卡爾合作,三人共同發展了圈量子引力理論。
這個理論涉及到一個積分,這個積分是沿著時空中的一些小圈而進行的,所以這個理論叫做“圈”量子引力,它沒有像惠勒-德威特方程那樣采用薛定諤方程,而是采取了海森堡方程的模式(需要找到一對正則變量來進行量子化)。該理論認為,時間和空間由離散的塊組成。物理學家定義了圈量子引力中基本單元的體積算符與面積算符,這些算符都有離散的本征值。這些最小的面積、體積不是連續變化的,因此該理論實現了時空的量子化。
圈量子引力概念圖
量子自旋網絡
前面說到,在圈量子引力中,空間是離散的。因此,三維空間可以被分成無數個基本的量子四面體。那么,物理學家如何刻畫這些量子四面體呢?這與1971年物理學家羅杰·彭羅斯提出的量子自旋網絡有關。
量子自旋網絡的構造用到了對偶的思想。如果存在一個多面體的空間量子,在量子自旋網絡中,可以用多面體的中心點表示這個多面體的體積,而用穿過各個表面的線條來表示其面積。
以下圖為例,a圖是一個正方體,假設這個正方體的邊長是2普朗克長度,那么每個面的面積是4個普朗克面積,這個正方體的體積是8個普朗克體積。因此,如果用量子自旋網絡來表示,那么就是b圖。圖上的這些數字,均與各個面對應的自旋有關。
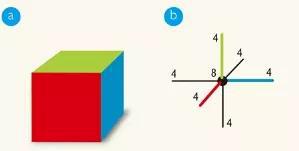
在圈量子力學的模型中,最基本的空間量子是一些量子四面體。這些量子四面體對應的量子自旋網絡如下圖所示。當然,這種量子四面體是在普朗克尺度下才出現的。對于量子四面體來說,其四個面的面積可以存在量子波動。
(邯鄲網站建設)
